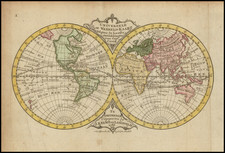
Nice example of prominent 18th-century mathematician and physicist Leonhard Euler's "Geographical Map of each Terrestrial Hemisphere showing the declination of the magnetic needle for Various places on the globe as of A.D. 1744."
This world map, depicting both the Eastern and Western Hemispheres, focuses on illustrating magnetic declination at various places on Earth as understood in the year 1744. Magnetic declination is the angle between magnetic north (the direction the north end of a compass needle points) and true north (the direction along Earth's surface towards the geographic North Pole). Magnetic declination varies depending on where one is located on the Earth's surface and changes over time due to fluctuations in the Earth's magnetic field.
The phenomenon was certainly recognized in the early 15th century, if not earlier. One of the first recorded discussions of magnetic declination is by the Portuguese navigator and explorer João de Castro, who noted it during his voyages in the Indian Ocean in the mid-16th century. English scientist William Gilbert provided the first thorough scientific study of the Earth's magnetism, including magnetic declination, in his seminal work "De Magnete," published in 1600. Gilbert is often credited with establishing the study of magnetism as a science, although he was not the first to discover magnetic declination itself.
At that time the map was made, understanding magnetic declination (which had first been explained by Sir Edmund Halley) was essential for accurately navigating the seas, as compasses rely on magnetic north. Mariners and explorers would need to know the local magnetic declination to correct their compass readings and ensure accurate navigation.
The note at the bottom center of the map translates as follows:
Since the magnetic needle's declination at the same places on Earth changes over time, Halley was the first to assemble this type of map for the year 1700, following the rules of nautical charts. Later, a similar map was published by William Mountaine and James Dodson in England, which represents the magnetic variations up to the year 1744. Since in nautical projection the true course of lines that are drawn through the same points of declination is more difficult to discern, it seemed advisable to display the same map in the usual way over both hemispheres of the earth: so that the connection and order of these lines can be more easily recognized at a glance.
The notes at the left and right translate as follows:
Each line that is seen on this map is drawn so that it passes through all the places on the earth where, in the year 1744, the magnetic needle experienced the same declination. Thus, the first line, drawn with a double path, indicates the places where the declination was zero. It rises from the southern regions through the Atlantic Ocean, crosses America above the Tropic of Cancer, and after crossing the Pacific Ocean, advances near the Japanese coasts, then with a remarkable bend, it returns through the Eastern Indies back into the southern regions from where, undoubtedly, it emerges again in an unknown path in the Atlantic Ocean, thus seeming to form a continuous line that returns into itself. Outside this line, the magnetic needle everywhere deviates, either to the east or to the west, as the map clearly shows where the eastern declinations are indicated by the letter E and the western declinations by the letter W (O for 'Occidentales').
In the upper hemisphere, the path of these lines towards the south seems quite regular, with a course straight according to the meridians directed towards the Antarctic Pole. However, due to the nature of things, it is impossible for any of these lines to be extended to the pole itself, because under the poles the distinction of the world's regions completely ceases. Whatever direction the magnetic needle holds there, no certain declination can be attributed to it, and for this reason, the continuation of these lines towards the poles is entirely unknown. In the lower hemisphere also, the course of these lines towards the south is found to be very disturbed and in no way is it clear how the lines begun in the western part should be continued without falling into manifest inconveniences. Around the North Pole, however, everything is still much more uncertain, except for Hudson's Bay.
Leonhard Euler, born on April 15, 1707, in Basel, Switzerland, stands as a towering figure in the history of mathematics and science. His prolific contributions span a wide range of fields including mathematics, physics, astronomy, and engineering. Recognized for his work in areas such as graph theory, topology, mechanics, fluid dynamics, and optics, Euler's influence is immeasurable, making him one of the greatest mathematicians of the 18th century and indeed, in history.
Euler's early life was steeped in academic and religious influence, with his father serving as a pastor and his mother coming from a line of scholars. His intellectual journey began under the guidance of his father and later, under the renowned mathematician Johann Bernoulli at the University of Basel. Despite his initial aspirations in theology, Euler's fascination with mathematics took precedence, leading to a lifelong dedication to the field.
His professional career was marked by significant periods in Saint Petersburg, Russia, and Berlin, Prussia. In Saint Petersburg, under the auspices of the Russian Academy of Sciences, Euler embarked on extensive scientific endeavors, contributing significantly to the academy's prestige. Despite political upheavals and personal challenges, including a near-fatal fever and deteriorating eyesight, Euler's productivity remained unparalleled. His tenure in Berlin, invited by Frederick the Great, was equally fruitful, yielding numerous works and fostering advancements in various disciplines, including map related projects.
Euler's contributions to mathematics are vast and diverse. He popularized and standardized many mathematical notations, such as the concept of a function and the symbols π, e (Euler's number), and i (the imaginary unit). His works in graph theory emerged from practical problems like the Seven Bridges of Königsberg, laying the foundation for this new field of mathematics. Euler also made groundbreaking contributions to the fields of number theory, calculus, and algebra, influencing countless areas of research and application.
In physics and engineering, Euler's insights transformed understanding and methodologies. His formulation of the Euler–Bernoulli beam equation marked a significant advancement in engineering, while his work in fluid dynamics and optics influenced subsequent theories and practices. Euler's contributions extended to astronomy, where his calculations improved celestial navigation and the understanding of cometary orbits.
Euler's personal life was characterized by his devout faith, simplicity, and resilience in the face of adversity. Despite suffering significant loss of eyesight, he continued his mathematical endeavors with the aid of assistants, demonstrating remarkable adaptability and perseverance. His return to Saint Petersburg in his later years saw continued scientific output until his death on September 18, 1783.
Euler's legacy is enduring, with his extensive body of work influencing countless fields and continuing to inspire future generations. His publications, which include more than 800 articles and numerous books, remain critical resources in mathematics and physics. Leonhard Euler's intellectual legacy is a testament to his unparalleled contribution to science and his enduring impact on the advancement of human knowledge.









![[Illuminated World Map -- There is no region of the world which Jesus, like the sun, does not enrich...] Orbis nulla plaga est quam sol non ditet Iesus...](https://storage.googleapis.com/raremaps/img/small/62347.jpg)